Sir Roger Penrose został niedawno ogłoszony zwycięzcą Nagrody Nobla. Choć Nobel jest z fizyki, Penrose jest blisko związany z Królową Nauk. Jak sam mówi, matematycy nazywają go fizykiem, a fizycy – matematykiem. To świetna okazja żeby zapoznać się bliżej z jednym z jego najsłynniejszych odkryć które leży na styku pomiędzy matematyką a… kafelkarstwem.
Piękno symetrii
Wyobraźmy sobie że chcemy pokryć podłogę kafelkami. Ponieważ nie chce nam się męczyć z układaniem skomplikowanych wzorów, postanówmy dodatkowo że układ płytek musi się regularnie powtarzać. Mówiąc nieco dokładniej, wymagamy aby układ płytek był niezmienny względem pewnego przesunięcia i pewnego obrotu (o kąt inny niż 360° i 180°). Na przykład, typowy układ kwadratowych płytek, widoczny na zdjęciu poniżej, nie zmieni się jeśli przesuniemy go o długość płytki w jednym z czterech podstawowych kierunków, ani kiedy obrócimy go o 90°.

Inna możliwość to, znany z natury, układ plastra miodu. Tu płytki są sześciokątami foremnymi, a ich układ pozostaje niezmieniony po obrocie o 120°. Możemy też każdy z sześciokątów podzielić na 6 trójkątów równobocznych – powstały podział jest niezmienny już przy obrocie o 60°. Jeśli ograniczamy się do kafelkowań przy użyciu wielokątów foremnych jednego typu, to by było na tyle: jedyne kształty którymi da się pokryć płaszczyznę to sześciokąty, kwadraty i trójkąty. Nie da się, na przykład, pokryć płaszczyzny pięciokątami foremnymi, i tak samo ma się sprawa z siedmiokątami, ośmiokątami, i tak dalej.

Jeśli dopuścimy więcej niż jeden rodzaj płytek, pojawia się naturalnie więcej możliwości. Możemy je uzyskać, między innymi, startując od wspomnianych wyżej kafelkowań i tnąc płytki na kawałki w regularny sposób – tak jak na ilustracjach poniżej. Nie pojawia się natomiast żaden nowy rodzaj symetrii: jedyne opcje to symetrie trzy-, cztero-, i sześcio-krotne, odpowiadające sześciokątom, kwadratom i trójkątom. Nie istnieje nadal symetryczne pokrycie płaszczyzny które byłby niezmienne po obrocie o, na przykład, 1/5 kąta pełnego.
Zalety niedoskonałości
Penrose odkrył sposób pokrycia płaszczyzny dwoma rodzajami rombów, którego fragment widoczny na ilustracji poniżej, o zaskakujących właściwościach.

Szybkie spojrzenie na rysunek sugeruje istnienie pewnych regularności – możemy na przykład zauważyć, że podobne układy powtarzają się częściej, niż tego byśmy się spodziewali gdyby płytki ułożone były na chybił-trafił. Bardziej dokładna analiza pokazuje że kafelkowanie Penrose’a ma przybliżoną symetrię ze względu na przesunięcia i obroty o 72°, czyli 1/5 pełnego kąta. To znaczy, istnieje takie przesunięcie, które pozostawi 90% płytek na swoich miejscach i „popsuje” co najwyżej 10% powierzchni; podobnie, istnienie przesunięcie które pozostawi na swoich miejscach 99% albo 99.9% płytek, i tak dalej. Nie istnieje jednak jedno przesunięcie które zachowa 100% płytek. Analogicznie, istnieją punkty wokół których obrót o 72° zmieni tylko niewielki odsetek płytek.
Taki stan rzeczy jest zaskakujący, ponieważ – jak pamiętamy z poprzedniej dyskusji – nie istnieje kafelkowanie które byłoby dokładnie niezmienne pod wpływem przesunięcia i obrotu o 72°. Fakt, że pozwalamy na bardzo nawet niewielki odsetek błędów pozwala nam na uzyskanie niemożliwego wcześniej typu symetrii!
Wymusić chaos
Kafelkowanie Penrose’a wiąże się z ciekawym problemem decyzyjnym. Wyobraźmy sobie że mamy do dyspozycji kilka kształtów płytek, i chcemy nimi pokryć płaszczyznę. Nie interesuje nas tu już żadna symetria – pytamy tylko, czy istnieje jakiekolwiek pokrycie. Na przykład, jeśli mamy do dyspozycji płytki w kształcie sześciokątów foremnych to takie pokrycie istnieje, a jeśli mamy zamiast tego pięciokąty to już nie.
Jeden z najprostszych sposobów żeby pokazać że dostępne nam płytki wystarczają do pokrycia płaszczyzny to najpierw pokryć nimi prostszy kształt, który da się później okresowo powtarzać. Na przykład, z puzzli o kształtach takich jak poniżej da się złożyć kwadrat, a kwadratami da się pokryć płaszczyznę – zatem da się też pokryć płaszczyznę puzzlami.

Przykłady takie jak powyżej rodzą pytanie – czy ta metoda zawsze działa? To znaczy – czy zawsze jest tak, że jeśli przy użyciu danego zestawu płytek da się pokryć płaszczyznę, to da się z tych płytek złożyć kształt którym da się pokryć płaszczyznę w sposób okresowy? Okazuje się nie. Pierwszy zestaw płytek dla którego istnieje pokrycie, ale nie istnieje pokrycie okresowe, został odkryty przez Roberta Bergera, i zawierał – bagatela! – 20426 płytek. Płytki Penrosa’a nie są jeszcze przykładem – używając tylko jednej z tych płytek, można pokryć płaszczyznę okresowo. Łatwo jest za to skonstruować przykład na ich podstawie: wystarczy wprowadzić zasady dotyczące tego, które krawędzie mogą się stykać. Można to zrobić tak jak na rysunku poniżej (pożyczonym z Wikipedii), wycinając i doklejając odpowiednie kształty do odpowiednich krawędzi – trochę tak jak w przypadku puzzli. Równoważnie, płytki muszą być złożone tak, aby niebieskie i czerwone łuki do siebie pasowały. Tak więc: z 20426 udało nam się zejść do 2.

Ciąć i rzutować
Chociaż rysunki przedstawiające kafelkowanie Penrose’a mają niewątpliwe walory estetyczne, nie mówią nam one skąd się ono wzięło ani jakie pomysły za nim stoją. Istnieje wiele metod konstrukcji takich quasi-okresowych układów. Można, na przykład… pożyczyć je z wyższych wymiarów.
Ponieważ wysoko-wymiarowe konstrukcje trudno jest zwizualizować, zacznijmy na rozgrzewkę od pokazania jak bardzo prosty podział płaszczyzny pozwala skonstruować ciekawy podział prostej. Zacznijmy od narysowania na płaszczyźnie siatki kwadratowej, albo raczej – jej wierzchołków, jak na ilustracji poniżej. Narysujmy też prostą i pas ograniczony liniami do niej równoległymi (zacieniowany obszar na rysunku). Rzutujmy następnie punkty wewnątrz wybranego pasa na naszą prostą i – voila! – otrzymaliśmy podział prostej na odcinki, który jest prawie (choć nie dokładnie) okresowy. W tej konstrukcji musimy odrobinę uważać którą prostą wybierzemy – nie każdy wybór jest dobry, niektóre prowadzą do okresowych podziałów: tak jest na przykład w przypadku prostej poziomej. Ale ponieważ prawie każdy wybór jest dobry, nie będziemy się zbytnio przejmować tym szczegółem technicznym.
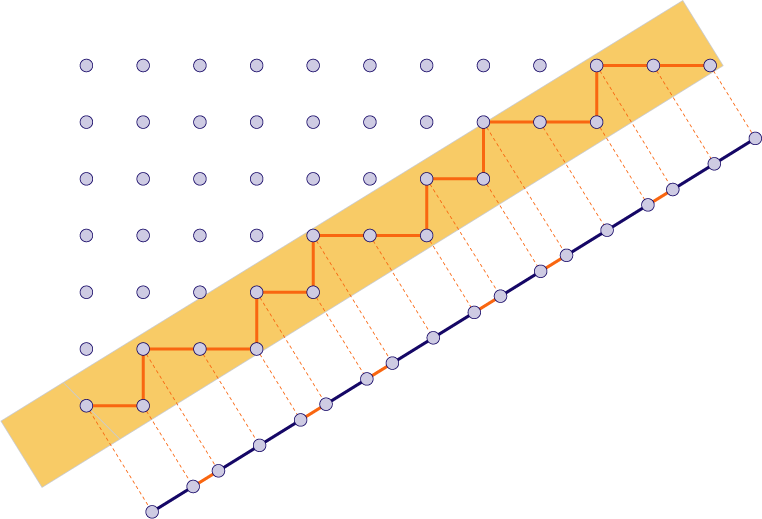
W wyższych wymiarach konstrukcja przebiega zupełnie analogicznie. Zaczynamy od prostego i symetrycznego układu punktów w przestrzeni trójwymiarowej lub wyższego wymiaru – choć trudno je sobie wyobrazić, ich matematyczny opis jest bardzo łatwy, po prostu mamy więcej współrzędnych. Wybieramy w tej przestrzeni płaszczyznę (bądź wyżej wymiarową podprzestrzeń) wraz z „pasem” który jest do naszej płaszczyzny równoległy. Rzutujemy prostopadle wszystkie punkty z pasa na płaszczyznę, i interpretujemy otrzymane rzuty jako wierzchołki naszych płytek. Symetrie z wyższego wymiaru można teraz przetłumaczyć na przybliżone symetrie rzutu.
Kafelkowanie Pensore’a można otrzymać przy wykorzystaniu powyższej konstrukcji, zaczynając od 5-wymiarowej przestrzeni. Jaki układ punktów w niej wybrać i jak zrzutować – to pozostawiamy dociekłości Czytelników.
Zastosowania praktyczne
Zainteresowanie kafelkowaniami takimi jak to znalezione przez Pensore’a nie wynika, jak Czytelnik zapewne się domyśla, z chęci wykładania płytek w fantazyjny sposób. Główna praktyczna motywacja do rozważań takich jak powyżej pochodzi z krystalografii, gdzie rolę płytek pełnią atomy, a rolę podłogi pełni trójwymiarowa przestrzeń. Układy płytek o przybliżonych symetriach odpowiadają tak zwanym quasikryształom – odkrytym stosunkowo niedawno materiałom, których dyfraktogramy wykazują „zakazane” symetrie. Ale to już historia na inną okazję.

