Niemal każdy z nas w dzieciństwie bawił się choć raz wańką-wstańką: zabawką która niezależnie od tego jak ją ustawimy, uparcie wraca do pionu. Za tą zaskakującą własnością stoi drobne oszustwo – w podstawie figurki znajduje się dodatkowa masa. W tym odcinku zapoznamy się z egzotyczną bryłą o nazwie Gömböc, która osiąga ten sam efekt nie uciekając się do tanich sztuczek.

Powód, dla którego wspomniana wyżej zabawka wraca do pionu, sprowadza się do tego, że jest to jej jedyne położenie równowagi stabilnej – to znaczy takiej, że jeśli odrobinę ją przechylimy, to wróci ona do poprzedniej pozycji. Wańka-wstańka ma też jedno położenie równowagi chwiejnej, gdzie figurka stoi na głowie – co prawda jest wówczas w równowadze, ale nawet najmniejsze zaburzenie wystarczy, żeby ją przewrócić. Dla innych brył może zdarzyć się również równowaga obojętna. Na przykład, dowolnie ustawiona idealna kula jest w takiej równowadze – jeśli lekko ją popchniemy, to trafimy w inny stan równowagi, który jest bliski wyjściowemu. Żeby nie komplikować sobie zanadto życia, ograniczymy się od teraz do przypadków, gdzie stany równowagi neutralnej nie występują.
Każda bryła ma przynajmniej jeden punkt równowagi – w przeciwnym razie pozostawałaby wiecznie w ruchu i stanowiłaby tym samym perpetuum mobile, które niestety wiadomo, że nie istnieje. Nieco bardziej skomplikowany argument dowodzi, że zawsze muszą istnieć co najmniej dwa punkty równowagi. Jak pokazuje powyższy przykład, to minimum da się zrealizować, przynajmniej jeśli pozwolimy na niejednorodny rozkład masy. Słynny Rosyjski matematyk, Vladimir Arnold, zapytał w 1995 roku czy istnieje bardziej eleganckie rozwiązanie, to znaczy bryła, która ma dokładnie dwa punkty równowagi i dodatkowo ma jednorodną gęstość i jest wypukła (to znaczy, z grubsza, pozbawiona jest dziur). I tak właśnie rozpoczęło się polowanie na Gömböc.
Dwa wymiary
Co zaskakujące, jeśli z trzech wymiarów przeniesiemy się na płaszczyznę, to odpowiedź na pytanie Arnolda jest negatywna: każda wypukła figura na płaszczyźnie ma przynajmniej cztery punkty równowagi.
Aby się o tym przekonać, zauważmy najpierw że jeśli figura jest w pozycji równowagi to środek masy leży pionowo nad punktem styczności z podłożem. Co za tym idzie, jeśli zmierzymy odległość punktów na krawędzi od środka masy, to w punktach równowagi ta odległość będzie przyjmowała wartości ekstremalne. Punkty równowagi stabilnej odpowiadają lokalnym minimom – innymi słowy, punktom na krawędzi, które są najbliżej środka masy jak to możliwe (przynajmniej jeśli ograniczymy się do pobliskich punktów brzegu). Przeciwnie, punkty równowagi chwiejnej to lokalne maksima. Wynika stąd, że punkty równowagi występują parami, na przemian stabilne i chwiejne.
Chcemy pokazać, że każda wypukła figura ma przynajmniej cztery punkty równowagi. Wyobraźmy sobie więc hipotetyczną figurę, która ma ich mniej – to znaczy, dokładnie dwa. Jak wynika z powyższych obserwacji, jeśli będziemy przesuwać się po brzegu, od punktu równowagi chwiejnej do punktu równowagi stabilnej, to nasza odległość od środka masy będzie stale maleć. Następny krok to znalezienie linii przechodzącej przez środek masy o tej własności, że ów środek masy leży dokładnie w połowie między dwoma punktami gdzie linia przecina brzeg naszej figury – jak na rysunku obok.
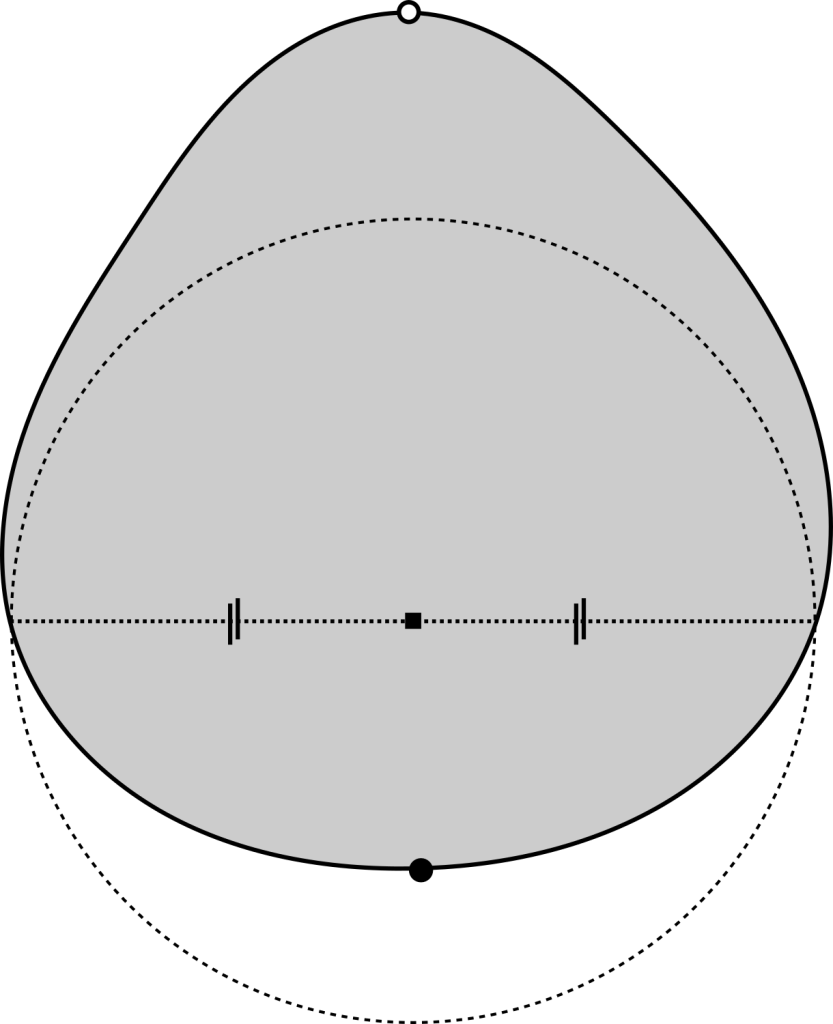
Środek równowagi zaznaczono kwadratem, zaś przerywaną kreską – linię podziału oraz okrąg, o których mowa w rozwiązaniu.
Ta linia dzieli naszą figurę na dwie części, i problemy zaczynają się kiedy spróbujemy porównać ich masy (lub, równoważnie, powierzchnie). Z jednej strony, linia podziału przecina środek masy całej figury, więc masy obu części muszą być równe. Z drugiej strony, możemy pokazać, że część leżąca po stronie punktu równowagi chwiejnej jest większa. Aby się o tym przekonać, można na przykład zauważyć, że zawiera ona półkole o średnicy takiej jak długość naszego cięcia, podczas gdy część leżąca po stronie punktu równowagi stabilnej cała zawiera się w tym półkolu.
Dotarliśmy zatem do sprzeczności, i co za tym idzie, hipotetyczna figura o dokładnie dwóch punktach równowagi istnieć nie może.
Gömböc
Wróćmy do oryginalnego, trójwymiarowego, problemu Arnolda. Droga do jego rozwiązania była niekonwencjonalna i zaczęła się … na plaży. Zainteresowany tym problemem węgierski matematyk Gábor Domokos wraz z żoną zebrali – bagatela! – 2 tysiące kamyków, po czym zbadali liczbę ich punktów stabilności, w nadziei, że przypadkiem trafią na bryłę, która ma dokładnie dwa. Niestety, nie znaleźli ani jednej.
Nie wynika stąd oczywiście że wspomniana bryła nie istnieje, jedynie że jest trudne do skonstruowania i rzadko występuje w przyrodzie. To sugeruje inną linię ataku. Zamiast szukać losowych i nieregularnych kształtów, Domokos oraz inny węgierski matematyk Péter Várkonyi przeprowadzili konstrukcję zaczynającą od najbardziej regularnego i nienaturalnego kształtu: od kuli. Modyfikując bardzo subtelnie jej brzeg, znaleźli oni wreszcie pierwszą w historii bryłę o opisanych przez Arnolda własnościach. Odkrytym w ten sposób kształtom nadali nazwę gömböc, od węgierskiego słowa gömb oznaczającego sferę. To samo słowo określa również … węgierskie dania przypominające ponoć kiełbasę (bądź szkocki haggis).

Pierwsza konstrukcja gömböca była wizualnie nierozróżnialna od sfery. Różnica wynosiła jedynie 0.001%, co przy bryle o średnicy jednego metra dawałoby 10 mikrometrów. W szczególności, stworzenie fizycznego modelu było praktycznie niewykonalne. Wielu matematyków by się w tym miejscu zatrzymało – wszak twierdzenie zostało udowodnione. Ale Domokos i Várkonyi uparli się stworzyć praktyczną reprezentację swoich wyników, co doprowadziło do znalezienia widocznego na zdjęciu, zdecydowanie nie-sferycznego kształtu (nazywanego czasem Gömböc, przez duże G). Obecnie ten gömböc można kupić w wielu sklepach, a w różnych zakątkach świata stoją pomniki w tym kształcie.

Zadanie domowe
Odkrycie gömböca ze zdjęcia powyżej to jeszcze nie koniec historii. Jest to wszak bardzo skomplikowana bryła, a problem od którego wyszliśmy wydaje się bardzo prosty. Czy można, na przykład, znaleźć wielościan o tych samych własnościach? Domokos and Várkonyi wyznaczyli nagrodę za znalezienie najprostszego możliwego z takich wielościanów. Jej wysokość to… miliona dolarów podzielone przez C, gdzie C to sumaryczna liczba ścian, krawędzi i wierzchołków znalezionej bryły. Jeśli C okaże się niewielkie, nagroda może być bardzo okazała. Kto wie, może któryś z Czytelników wpadnie na pomysł?